在图像处理时,我们会经常需要判断一个点是否位于多边形区域内。比较好用的是射线法。
射线法
算法思想非常巧妙:从待判断的点向某一个方向引射线,计算和多边形交点的个数,如果个数是偶数或者0则点在多边形外,如果是奇数,则在多边形内,如下图:
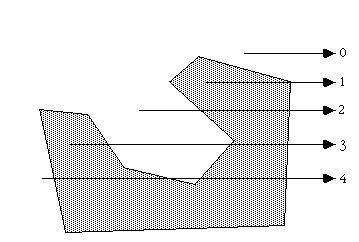
这里有二种特殊情况:
|
|
1. 射线经过顶点:当射线经过顶点时,判断就会出现异常情况。 2. 点在边上:这种情况也不能用交点个数的奇偶性来判断了,要快速地判断这个点是否在边上。 |
C的实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
#define MIN(x,y) (x < y ? x : y) #define MAX(x,y) (x > y ? x : y) typedef struct { double x,y; } Point; int InsidePolygon(Point *polygon,int N,Point p) { int counter = 0; int i; double xinters; Point p1,p2; p1 = polygon[0]; for (i=1;i<=N;i++) { p2 = polygon[i % N]; if (p.y > MIN(p1.y,p2.y)) { //低 if (p.y <= MAX(p1.y,p2.y)) { //高 if (p.x <= MAX(p1.x,p2.x)) { //右 if (p1.y != p2.y) { //简单忽略平行X轴这种情况 xinters = (p.y-p1.y)*(p2.x-p1.x)/(p2.y-p1.y)+p1.x; //交叉点坐标 参考./media/point-and-polygon/xinters.jpg if (p1.x == p2.x || p.x <= xinters) counter++; } } } } p1 = p2; } if (counter % 2 == 0) return 0; else return 1; } |
再来个C#版的
|
|
public static bool Contains( Point[] points, Point p ) { bool result = false; for( int i = 0; i < points.Length - 1; i++ ) { if( ( ( ( points[ i + 1 ].Y <= p.Y ) && ( p.Y < points[ i ].Y ) ) || ( ( points[ i ].Y <= p.Y ) && ( p.Y < points[ i + 1 ].Y ) ) ) && ( p.X < ( points[ i ].X - points[ i + 1 ].X ) * ( p.Y - points[ i + 1 ].Y ) / ( points[ i ].Y - points[ i + 1 ].Y ) + points[ i + 1 ].X ) ) { result = !result; } } return result; } |
值得一提的是射线法对于带岛的多边形依然有效:
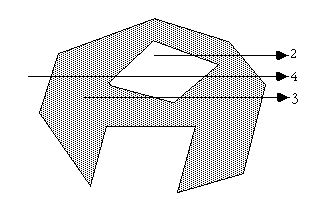
改进:传统的射线法一开始就直接计算点和多边形的交点个数,这样的话,会花费大量的时间来作拓扑关系的判断,我们可以首先计算出最小外包矩形,迅速排除不在矩形内部的点,然后再做上面的判断。

