GPU IS a processor (graphics proccessing unit). Anywho, i remember seeing somewhere that in geforce 6 series cards its a signle cycle (maybe i was just dreaming :-p) but i have that memory
radeon x800 has it anyways
EDIT:
Quote:
ORIGINALLY AT: http://gear.ibuypower.com/GVE/Store/ProductDetails.aspx?sku=VC-POWERC-147
Smartshader HD•Support for Microsoft® DirectX® 9.0 programmable vertex and pixel shaders in hardware
• DirectX 9.0 Vertex Shaders
- Vertex programs up to 65,280 instructions with flow control
- Single cycle trigonometric operations (SIN & COS)
• Direct X 9.0 Extended Pixel Shaders
- Up to 1,536 instructions and 16 textures per rendering pass
- 32 temporary and constant registers
- Facing register for two-sided lighting
- 128-bit, 64-bit & 32-bit per pixel floating point color formats
- Multiple Render Target (MRT) support
• Complete feature set also supported in OpenGL® via extensions
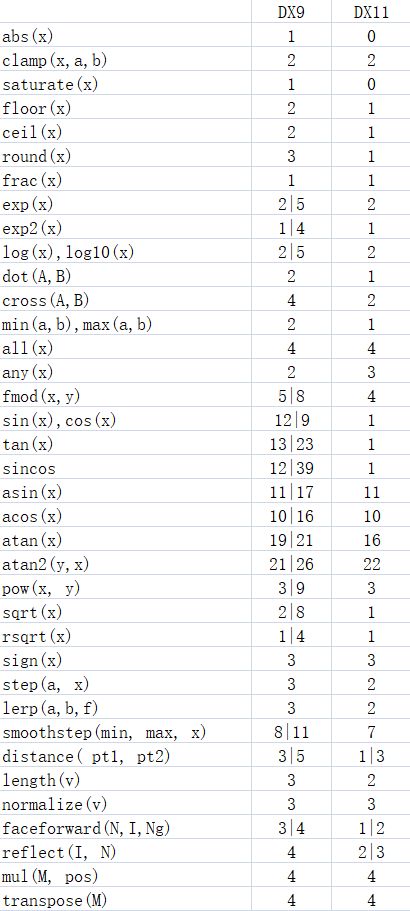
I was thinking of making a tool to calculate the computational cost of a line of shader code. The tool would then output the cost value for each line of code, possibly colouring the line of code to represent how expensive it is. As we have discussed previously, it is difficult to gauge exactly how computationally expensive a particular shader function (refering to the intrinsic functions, min, max, sin, cos, .etc) is going to be.
But I believe you can make reasonable assumptions about the cost of a function. Actually, what I believe is important here is the ordering of cost w.r.t other functions. It should be reasonable to assume that the cost of evaluating the sine of an angle is more computational work than the cost of adding two scalars.
Here are some example costs that would be the basis for the calculation, which would just be a simple walk over the operations, and adding the operation cost to a total for that line number in the code. I expect that the numbers would be configurable in the tool anyhow:
| scalar add,sub,mult,div | 1 | |
| vec4 add/mul/div/sub | 4*1 | |
| scalar fract() | 2 | |
| scalar sqrt() | 2 | |
| vec3 dot() | 3 | |
| vec3 normalize() | 5 | (dot + sqrt) |
| scalar sin() | 2+3 | (fract + dot) |
| vec4 sin() | 4*(3+2) | (4 * sin) |
| mat4 * vec3 | 4*3 | (4 * dot) |
| mat4 * mat4 | 4*4*3 | (4 * 4 * dot) |
In general, the cost of a n-vector operation is simply n * (cost of scalar operation), with some assumptions made about when these operations can be reduced to dot or fmaoperations. Also, for a branch, only the operations that make up the condition would count towards the cost.
Do you think these numbers make sense? Is there a better formula that could be applied to compute the cost of an individual line of code, as a function of the cost of it's individual operations?
The cost of some operations can vary depending on the GPU manufacturer and the architecture. This is what I could dig up. I might be wrong about some of the Nvidia stuff- I tried to guess as best as I could from the architectural details Nvidia has released. AMD was dead simple, though.
For both Nvidia and AMD:
Add, Multiply, Subtract and MAD/FMA - 1
For AMD:
1/x, sin(x), cos(x), log2(x), exp2(x), 1/sqrt(x) - 4
x/y - 5 (one reciprocal, one mul)
sqrt(x) - probably 5 (one reciprocal square root, one mul)
For Nvidia Fermi architecture (GeForce 400 and 500 series) :8
1/x, sin(x), cos(x), log2(x), exp2(x), 1/sqrt(x)
Edit: not quite sure how large the dispatch overhead is for these operations on Fermi... anyway, throughput for these functions is 1/8 the speed of normal ops, so try to limit these functions to 1/9 of all total ops on average.
For Nvidia Kepler (GeForce 700 series) and Maxwell architecture (800M and 900 series):
1/x, sin(x), cos(x), log2(x), exp2(x), 1/sqrt(x) - 0 or close to 0, as long as they are limited to 1/9 of all total ops (can go up to 1/5 for Maxwell).
x/y - 1 (one special op, one mul)
sqrt(x) - 1 (one special op, one mul)
(obviously, for vector versions of the above functions, multiply by the width of the vector)
For all GPU's:
vec3 dot - 3
vec3 normalize - 6 + cost of a "1/sqrt(x)" op
asin, acos, atan - LOTS, probably around 25 (no native support on either Nvidia or AMD, so they emulate it in software).
Also, I think a conditional branch does come with some fixed overhead, but I don't know how much.
Reasons for my Nvidia numbers:
The reason for the "0" for various "special functions" (1/x, sin x, etx) on Nvidia Kepler/Maxwell, is because those functions are computed on a separate hardware (special functions unit, or SFU) unit in parallel to standard operations. Throughput is 1/8 that of standard ops (1/4 on Maxwell), so if your code has too many of those ops, they'll become a bottleneck. Hence the 1/9 and 1/5 guidelines. On Fermi, there is still a separate SFU for those functions, but due to the way instruction dispatching works, it looks like there might be some non-negligible overhead, but I'm not sure how much.
So with these SFU's, are you suggesting that sin,cos,tan and transcendentals be assigned a cost of 1? It sounds kind of suspicious, I'm sure I've seen sine and cosine be expanded into it's Taylor series by HLSL (admittedly, not GLSL) constant folding.
For simplicity sake, and to keep things meaningful on a lot of machines, the operation cost could, instead, be defined in terms of the number of vector elements operated on. That would be consistent with your proposal, where scalar sine is 1.
Under this scheme, the example costs from the table become:
| scalar add,sub,mult,div | 1 |
| vec4 add/mul/div/sub | 4 |
| scalar fract() | 1 |
| scalar sqrt() | 1 |
| vec3 dot() | 3 |
| vec3 normalize() | 3 |
| scalar sin() | 1 |
| vec4 sin() | 4 |
| mat3 * vec3 | 3*3 |
| mat4 * mat4 | 4*4*4 |
Interesting points about the inability to predict the behaviour of loops. I think the GLSL version 100 requires that loops be predictable in some way, I've not yet looked at it in detail. But there would be no way to know that a loop will exit-early every time.
As for the code, I expect to make it available at some point, if the thing turns out to be at all useful. I've been told there are tools by nvidia that already do static analysis, which will be better than anything I can put together.