0、参考链接
|
1 2 3 4 5 6 7 8 |
密码行业标准化技术委员会 http://www.gmbz.org.cn/main/bzlb.html SM2密码算法使用规范 http://www.gmbz.org.cn/main/viewfile/2018011001400692565.html SM2密码算法应用分析 https://blog.csdn.net/arlaichin/article/details/23708155?utm_source=itdadao&utm_medium=referral 技术科普 | 国密算法在Ultrain区块链中的运用 https://blog.csdn.net/Tramp_1/article/details/111603396 |
1、SM2数字信封格式:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
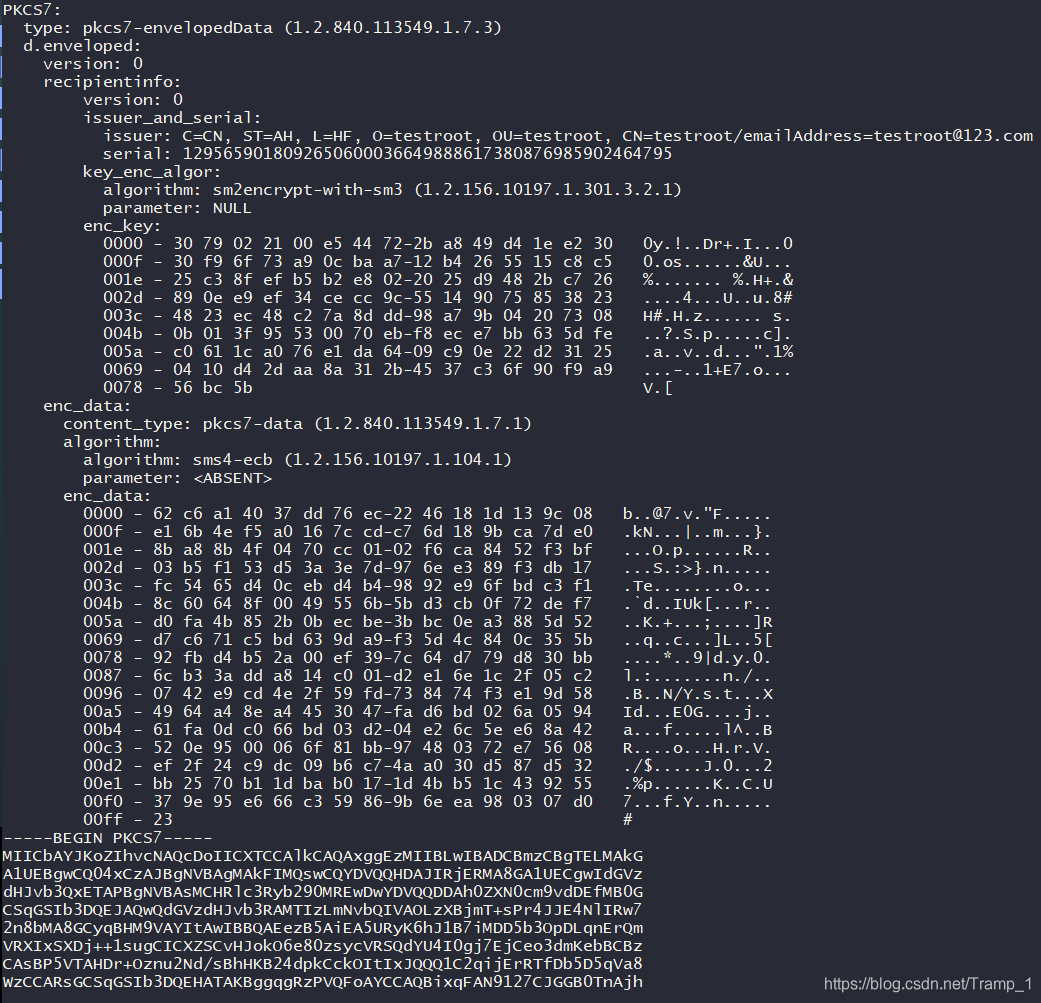
有效部分 公钥:04|X|Y,共65字节 私钥:整数,共32字节 SM2EnvelopedKey ::= SEQUENCE { symalgid AlgorithmIdentifier, -- 对称算法ID symalgkey SM2Cipher, -- 对称算法密钥(被签名证书公钥加密) asympubkey BIT STRING, -- 加密证书公钥 asymprvkey BIT STRING -- 加密证书私钥(被对称算法加密) } typedef struct SM2Cipher_st { ASN1_INTEGER *xCoordinate; // x分量(随机,非公钥) ASN1_INTEGER *yCoordinate; // y分量(随机,非公钥) ASN1_OCTET_STRING *hash; // 杂凑值 ASN1_OCTET_STRING *cipherText; // 密文 } SM2Cipher; AlgorithmIdentifier ::= SEQUENCE { algorithm OBJECT IDENTIFIER, parameters ANY DEFINED BY algorithm OPTIONAL } 区分普通的数字信封格式,见下图(openssl暂不支持SM2算法的私钥P7信封格式生成,但是支持SM2算法私钥的P7解密,生成P7可以在外部使用gmssl命令行生成) typedef struct pkcs7_enveloped_st { ASN1_INTEGER *version; /* version 0 */ STACK_OF(PKCS7_RECIP_INFO) *recipientinfo; PKCS7_ENC_CONTENT *enc_data; } PKCS7_ENVELOPE; typedef struct pkcs7_recip_info_st { ASN1_INTEGER *version; /* version 0 */ PKCS7_ISSUER_AND_SERIAL *issuer_and_serial; X509_ALGOR *key_enc_algor; ASN1_OCTET_STRING *enc_key; X509 *cert; /* get the pub-key from this */ const PKCS7_CTX *ctx; } PKCS7_RECIP_INFO; typedef struct pkcs7_enc_content_st { ASN1_OBJECT *content_type; X509_ALGOR *algorithm; ASN1_OCTET_STRING *enc_data; /* [ 0 ] */ const EVP_CIPHER *cipher; const PKCS7_CTX *ctx; } PKCS7_ENC_CONTENT; typedef struct pkcs7_st { /* * The following is non NULL if it contains ASN1 encoding of this * structure */ unsigned char *asn1; long length; # define PKCS7_S_HEADER 0 # define PKCS7_S_BODY 1 # define PKCS7_S_TAIL 2 int state; /* used during processing */ int detached; ASN1_OBJECT *type; /* content as defined by the type */ /* * all encryption/message digests are applied to the 'contents', leaving * out the 'type' field. */ union { char *ptr; /* NID_pkcs7_data */ ASN1_OCTET_STRING *data; /* NID_pkcs7_signed */ PKCS7_SIGNED *sign; /* NID_pkcs7_enveloped */ PKCS7_ENVELOPE *enveloped; /* NID_pkcs7_signedAndEnveloped */ PKCS7_SIGN_ENVELOPE *signed_and_enveloped; /* NID_pkcs7_digest */ PKCS7_DIGEST *digest; /* NID_pkcs7_encrypted */ PKCS7_ENCRYPT *encrypted; /* Anything else */ ASN1_TYPE *other; } d; PKCS7_CTX ctx; } PKCS7; |
2、代码中SM2数字信封加密解密步骤
|
1 2 3 4 5 6 7 8 9 10 11 |
1、将加密证书私钥转换为DER格式(二进制) 2、设置对称算法ID,公钥有效数据部分,私钥有效数据部分 对称算法ID默认为0x2A, 0x81, 0x1C, 0xCF, 0x55, 0x01, 0x68, 0x01(即SM4_ECB,1.2.156.10197.1.104.1) 公钥数据前缀为0xA1, 0x44, 0x03, 0x42, 0x00,截取65字节明文 私钥数据前缀为0x02, 0x01, 0x01, 0x04, 0x20,截取32字节明文 3、创建对称密钥,加密私钥有效数据部分 使用SM4_ECB算法和创建的128位随机密钥,加密私钥32字节得到32字节密文 4、使用签名公钥加密对称密钥,密文转换为二进制 使用SM2算法加密128位对称密钥,得到对称密钥密文(此处我使用了openssl已实现的SM2算法加密,因此不需要按照国标文档里深入底层计算预处理结果) 5、将对称算法ID,对称密钥密文,公钥,私钥密文转换为信封格式数据(此处可以参考openssl内部代码实现结构体和i2d格式转换) 6、将DER二进制信封转换为PEM格式(Base64),输出 |
解密(将SM2数字信封格式转换为加密私钥)
|
1 2 3 4 5 6 7 8 9 10 11 |
1、P7(PEM格式)转二进制 2、解析二进制,得到对称算法ID,对称算法密钥密文,加密证书公钥,加密证书私钥密文二进制 3、对称算法ID转具体算法名称 二进制字符串ID转换为OID(1.2.156.10197.1.104.1)进行匹配 4、签名私钥解密,得到对称算法密钥 使用SM2算法解密对称密钥密文,得到对称密钥明文 5、对称算法解密,得到加密私钥有效数据,32字节 使用SM4_ECB算法和对称密钥明文,解密私钥32字节密文得到32字节明文 6、拼接公钥,私钥得到完整加密私钥der二进制格式,有两种方式(此处拼接方法是我自己创造的,有什么其他好方法欢迎共享) (1)"30770201010420" + 32字节私钥 + "A00A06082A811CCF5501822DA144034200" + 65字节公钥 (2)"308187020100301306072A8648CE3D020106082A811CCF5501822D046D306B0201010420" + 32字节私钥 + "A144034200" + 65字节公钥 7、转换DER得到PEM格式文件 |
3、SM2数字信封格式详解
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
P7 PEM格式(Base64) MIHtMAkGByqBHM9VAWgweQIgMtHF6qRZOKJxnT5MYSv4eK/LjJHmp7b/p7AaP6cqigkCIQCFpr2MmakaMxVH1u+Yzxf+oJSFETwiZacB4j3NohlbHwQgO50Hic8tDYBLedIbuqsS2lXvPDYtyuLUrQKyGRI1Y9gEEA5lnd3Yxujfedxk6Cam9ygDQgAEnrxloYKoCRYc3Lh96OYupmT7V7X/BBgdcfCMQnsB7nQhD6FVwgKoN0JMwMqHXGg6l891FCfuTh5N51YqOAqBwwMhAHiB9UgemN+Xz39qsdMeVl4SKdmHHkPkKmNOBJjoqHor P7二进制 3081ED300906072A811CCF5501683079022032D1C5EAA45938A2719D3E4C612BF878AFCB8C91E6A7B6FFA7B01A3FA72A8A0902210085A6BD8C99A91A331547D6EF98CF17FEA09485113C2265A701E23DCDA2195B1F04203B9D0789CF2D0D804B79D21BBAAB12DA55EF3C362DCAE2D4AD02B219123563D804100E659DDDD8C6E8DF79DC64E826A6F728034200049EBC65A182A809161CDCB87DE8E62EA664FB57B5FF04181D71F08C427B01EE74210FA155C202A837424CC0CA875C683A97CF751427EE4E1E4DE7562A380A81C30321007881F5481E98DF97CF7F6AB1D31E565E1229D9871E43E42A634E0498E8A87A2B 主要包含(1)(2)(3)(4) 3081ED30090607 (1)对称算法ID:SM4 2A811CCF550168 (2)对称算法密钥密文(SM2加密): 3079022032d1c5eaa45938a2719d3e4c612bf878afcb8c91e6a7b6ffa7b01a3fa72a8a0902210085a6bd8c99a91a331547d6ef98cf17fea09485113c2265a701e23dcda2195b1f04203b9d0789cf2d0d804b79d21bbaab12da55ef3c362dcae2d4ad02b219123563d804100e659dddd8c6e8df79dc64e826a6f728 拆解后: 30790220 x:32d1c5eaa45938a2719d3e4c612bf878afcb8c91e6a7b6ffa7b01a3fa72a8a09 022100 y:85a6bd8c99a91a331547d6ef98cf17fea09485113c2265a701e23dcda2195b1f 0420 m:3b9d0789cf2d0d804b79d21bbaab12da55ef3c362dcae2d4ad02b219123563d8 0410 c:0e659dddd8c6e8df79dc64e826a6f728 (c结构密文) 04|x|y|m|c 0432D1C5EAA45938A2719D3E4C612BF878AFCB8C91E6A7B6FFA7B01A3FA72A8A0985A6BD8C99A91A331547D6EF98CF17FEA09485113C2265A701E23DCDA2195B1F3B9D0789CF2D0D804B79D21BBAAB12DA55EF3C362DCAE2D4AD02B219123563D80E659DDDD8C6E8DF79DC64E826A6F728 使用SM2签名私钥解密(2)后得到 对称密钥明文:EP/+Xo55MBhI3e1GTyghhQ==:10FFFE5E8E79301848DDED464F282185 (3)加密证书公钥: 034200 有效数据明文(65B):049ebc65a182a809161cdcb87de8e62ea664fb57b5ff04181d71f08c427b01ee74210fa155c202a837424cc0ca875c683a97cf751427ee4e1e4de7562a380a81c3 (4)加密证书私钥(加密): 032100 有效数据密文(32B):7881f5481e98df97cf7f6ab1d31e565e1229d9871e43e42a634e0498e8a87a2b 使用(2)中对称密钥解密得到SM2私钥有效数据明文 cipher.txt.bin:7881f5481e98df97cf7f6ab1d31e565e1229d9871e43e42a634e0498e8a87a2b #需要将十六进制转换为二进制文件 openssl enc -d -sm4-ecb -in cipher.txt.bin -K 10FFFE5E8E79301848DDED464F282185 -p -out plain.txt.bin #解密得到明文 加密验证 plain.txt.bin:71e49d78b44c6fd54331869f343c537c0a736954ae22cd50277ae587a7e6762e #需要将十六进制转换为二进制文件 openssl enc -e -sm4-ecb -nopad -in plain.txt.bin -K 10FFFE5E8E79301848DDED464F282185 -p -out cipher.txt.bin #使用明文加密得到 加密证书公钥DER: 3059301306072a8648ce3d020106082a811ccf5501822d034200 049ebc65a182a809161cdcb87de8e62ea664fb57b5ff04181d71f08c427b01ee74210fa155c202a837424cc0ca875c683a97cf751427ee4e1e4de7562a380a81c3 加密证书私钥DER(格式1): 308187020100301306072A8648CE3D020106082A811CCF5501822D046D306B0201010420 私钥有效数据 71E49D78B44C6FD54331869F343C537C0A736954AE22CD50277AE587A7E6762E A144034200 公钥有效数据049EBC65A182A809161CDCB87DE8E62EA664FB57B5FF04181D71F08C427B01EE74210FA155C202A837424CC0CA875C683A97CF751427EE4E1E4DE7562A380A81C3 加密证书私钥DER(格式2): 30770201010420 私钥有效数据 71e49d78b44c6fd54331869f343c537c0a736954ae22cd50277ae587a7e6762e a00a06082a811ccf5501822d a144034200 公钥有效数据 049ebc65a182a809161cdcb87de8e62ea664fb57b5ff04181d71f08c427b01ee74210fa155c202a837424cc0ca875c683a97cf751427ee4e1e4de7562a380a81c3 |