上节介绍了如何使用起泡排序的思想对无序表中的记录按照一定的规则进行排序,本节再介绍一种排序算法——快速排序算法(Quick Sort)。
C语言中自带函数库中就有快速排序——qsort函数 ,包含在 <stdlib.h> 头文件中。
快速排序算法是在起泡排序的基础上进行改进的一种算法,其实现的基本思想是:通过一次排序将整个无序表分成相互独立的两部分,其中一部分中的数据都比另一部分中包含的数据的值小,然后继续沿用此方法分别对两部分进行同样的操作,直到每一个小部分不可再分,所得到的整个序列就成为了有序序列。
例如,对无序表{49,38,65,97,76,13,27,49}进行快速排序,大致过程为:
- 首先从表中选取一个记录的关键字作为分割点(称为“枢轴”或者支点,一般选择第一个关键字),例如选取 49;
- 将表格中大于 49 个放置于 49 的右侧,小于 49 的放置于 49 的左侧,假设完成后的无序表为:
{27,38,13,49,65,97,76,49}; - 以 49 为支点,将整个无序表分割成了两个部分,分别为
{27,38,13}和{65,97,76,49},继续采用此种方法分别对两个子表进行排序; - 前部分子表以 27 为支点,排序后的子表为
{13,27,38},此部分已经有序;后部分子表以 65 为支点,排序后的子表为{49,65,97,76}; - 此时前半部分子表中的数据已完成排序;后部分子表继续以 65为支点,将其分割为
{49}和{97,76},前者不需排序,后者排序后的结果为{76,97}; - 通过以上几步的排序,最后由子表
{13,27,38}、{49}、{49}、{65}、{76,97}构成有序表:{13,27,38,49,49,65,76,97};
整个过程中最重要的是实现第 2 步的分割操作,具体实现过程为:
- 设置两个指针 low 和 high,分别指向无序表的表头和表尾,如下图所示:

- 先由 high 指针从右往左依次遍历,直到找到一个比 49 小的关键字,所以 high 指针走到 27 的地方停止。找到之后将该关键字同 low 指向的关键字进行互换:

- 然后指针 low 从左往右依次遍历,直到找到一个比 49 大的关键字为止,所以 low 指针走到 65 的地方停止。同样找到后同 high 指向的关键字进行互换:

- 指针 high 继续左移,到 13 所在的位置停止(13<49),然后同 low 指向的关键字进行互换:

- 指针 low 继续右移,到 97 所在的位置停止(97>49),然后同 high 指向的关键字互换位置:
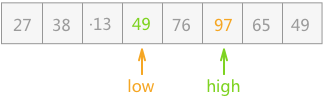
- 指针 high 继续左移,此时两指针相遇,整个过程结束;
该操作过程的具体实现代码为:
该方法其实还有可以改进的地方:在上边实现分割的过程中,每次交换都将支点记录的值进行移动,而实际上只需在整个过程结束后(low==high),两指针指向的位置就是支点记录的准确位置,所以无需每次都移动支点的位置,最后移动至正确的位置即可。
所以上边的算法还可以改写为:
快速排序的完整实现代码(C语言)
运行结果:
总结
快速排序算法的时间复杂度为O(nlogn),是所有时间复杂度相同的排序方法中性能最好的排序算法。