最近在看"程序员的数学"系列的"线性代数"部分，当阅读向量矩阵乘法的时候，感觉各种别扭。以前学习的时候，简单的把向量乘以矩阵简化理解成矩阵乘以一维矩阵，然后交换位置进行矩阵乘法。也就是 n 维向量乘以 m*n 矩阵，变成m*n 矩阵乘以 n*1 维矩阵。以后一直是这么计算的。
这么理解计算结果是正确的，但是却不利于理解矩阵的映射特性，矩阵就是映射 这句话怎么都理解不对了！！
书本中一直说向量是竖排的，类似这样 $\begin{bmatrix} v1\\\ v2\\\ v3\\\ v4 \end{bmatrix}$。
并且说 n 维向量乘以 m*n 矩阵，得到 m 维向量。这个各种不理解，把列向量理解成了列矩阵，因此这个乘法各种不理解，不符合矩阵的运算规则。这么多年过去了，基础知识都理解的不正确，呵呵！！
其实，书上 1.16部分已经解释过，列向量计算的时候，要放倒，变成 $\begin{bmatrix} v1& v2& v3& v4 \end{bmatrix}$ 的样子，再参与计算。计算结果再切换成$\begin{bmatrix} v1\\\ v2\\\ v3\\\ v4 \end{bmatrix}$的列向量的样子，这样就可以完整的理解整个映射过程了。
1、向量乘以矩阵
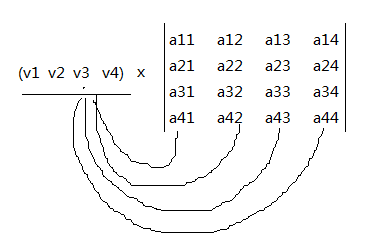
如上图所示，是用向量的各个元素，乘以矩阵的对应列的四个分量，得到最终的向量，程序如下：
public Vector4 Mul(Vector4 v)
{
Vector4 newV = new Vector4();
newV.x = v.x * this[1, 1] + v.y * this[2, 1] + v.z * this[3, 1] + v.w * this[4, 1];
newV.y = v.x * this[1, 2] + v.y * this[2, 2] + v.z * this[3, 2] + v.w * this[4, 2];
newV.z = v.x * this[1, 3] + v.y * this[2, 3] + v.z * this[3, 3] + v.w * this[4, 3];
newV.w = v.x * this[1, 4] + v.y * this[2, 4] + v.z * this[3, 4] + v.w * this[4, 4];
return newV;
}
2、矩阵乘以矩阵
矩阵的相乘，以4*4矩阵为例子，为什么选择4*4呢，因为3D图形学中最常用到的就是4阶矩阵。
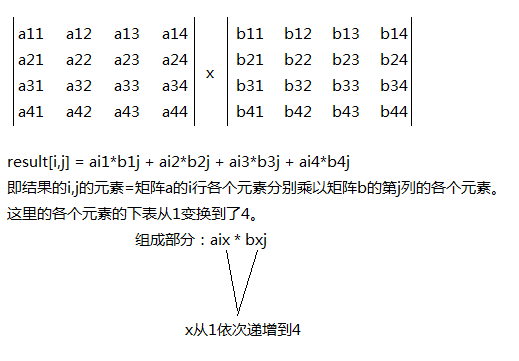
所以又所以，我们苦思冥想，怎么用程序实现呢？哈哈，不要捉急，知识一方面是创新，但也有一方面是cp。cp之后，理解就好。
ok，程序如下：
public Matrix4x4 Mul(Matrix4x4 m)
{
Matrix4x4 newM = new Matrix4x4();
for(int i=1;i<=4;++i)
{
for(int j=1;j<=4;++j)
{
for(int k=1;k<=4;++k)
{
newM[i, j] += this[i, k] * m[k, j];
}
}
}
return newM;
}